Рекурсия, стек

В теле функции могут быть вызваны другие функции для выполнения подзадач.

Частный случай подвызова – когда функция вызывает сама себя. Это называется рекурсией.

Рекурсия используется для ситуаций, когда выполнение одной сложной задачи можно представить как некое действие в совокупности с решением той же задачи в более простом варианте.

Сейчас мы посмотрим примеры.

Рекурсия – общая тема программирования, не относящаяся напрямую к JavaScript. Если вы разрабатывали на других языках или изучали программирование раньше в ВУЗе, то наверняка уже знаете, что это такое.

Эта глава предназначена для читателей, которые пока с этой темой незнакомы и хотят лучше разобраться в том, как работают функции.

Степень pow(x, n) через рекурсию

В качестве первого примера использования рекурсивных вызовов – рассмотрим задачу возведения числа x в натуральную степень n.

Её можно представить как совокупность более простого действия и более простой задачи того же типа вот так:

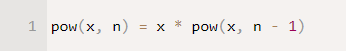
То есть, xn = x * xn-1.

Например, вычислим pow(2, 4), последовательно переходя к более простой задаче:

1. pow(2, 4) = 2 * pow(2, 3)
2. pow(2, 3) = 2 * pow(2, 2)
3. pow(2, 2) = 2 * pow(2, 1)
4. pow(2, 1) = 2

На шаге 1 нам нужно вычислить pow(2,3), поэтому мы делаем шаг 2, дальше нам нужно pow(2,2), мы делаем шаг 3, затем шаг 4, и на нём уже можно остановиться, ведь очевидно, что результат возведения числа в степень 1 – равен самому числу.

Далее, имея результат на шаге 4, он подставляется обратно в шаг 3, затем имеем pow(2,2) – подставляем в шаг 2 и на шаге 1 уже получаем результат.

Этот алгоритм на JavaScript:

Говорят, что «функция pow рекурсивно вызывает сама себя» до n == 1.

Значение, на котором рекурсия заканчивается, называют базисом рекурсии. В примере выше базисом является 1.

Общее количество вложенных вызовов называют глубиной рекурсии. В случае со степенью, всего будет n вызовов.

Максимальная глубина рекурсии в браузерах ограничена, точно можно рассчитывать на 10000 вложенных вызовов, но некоторые интерпретаторы допускают и больше.

Итак, рекурсию используют, когда вычисление функции можно свести к её более простому вызову, а его – ещё к более простому, и так далее, пока значение не станет очевидно.

Контекст выполнения, стек

Теперь мы посмотрим, как работают рекурсивные вызовы. Для этого мы рассмотрим, как вообще работают функции, что происходит при вызове.

У каждого вызова функции есть свой «контекст выполнения» (execution context).

Контекст выполнения – это служебная информация, которая соответствует текущему запуску функции. Она включает в себя локальные переменные функции и конкретное место в коде, на котором находится интерпретатор.

Например, для вызова pow(2, 3) из примера выше будет создан контекст выполнения, который будет хранить переменные x = 2, n = 3. Мы схематично обозначим его так:

• Контекст: { x: 2, n: 3, строка 1 }

Далее функция pow начинает выполняться. Вычисляется выражение n != 1 – оно равно true, ведь в текущем контексте n=3. Поэтому задействуется первая ветвь if :

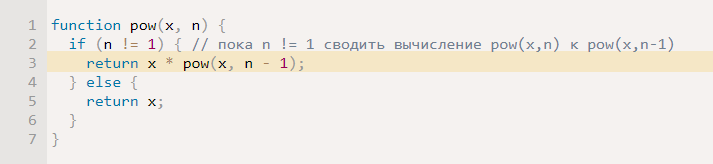
Чтобы вычислить выражение x * pow(x, n-1), требуется произвести запуск pow с новыми аргументами.

При любом вложенном вызове JavaScript запоминает текущий контекст выполнения в специальной внутренней структуре данных – «стеке контекстов».

Затем интерпретатор приступает к выполнению вложенного вызова.

В данном случае вызывается та же pow, однако это абсолютно неважно. Для любых функций процесс одинаков.

Для нового вызова создаётся свой контекст выполнения, и управление переходит в него, а когда он завершён – старый контекст достаётся из стека и выполнение внешней функции возобновляется.

Разберём происходящее с контекстами более подробно, начиная с вызова (*):

pow(2, 3)

Запускается функция pow, с аргументами x=2, n=3. Эти переменные хранятся в контексте выполнения, схематично изображённом ниже:

• Контекст: { x: 2, n: 3, строка 1 }

Выполнение в этом контексте продолжается, пока не встретит вложенный вызов в строке 3.

pow(2, 2)

В строке 3 происходит вложенный вызов pow с аргументами x=2, n=2. Текущий контекст сохраняется в стеке, а для вложеннного вызова создаётся новый контекст (выделен жирным ниже):

• Контекст: { x: 2, n: 3, строка 3 }
• Контекст: { x: 2, n: 2, строка 1 }

Обратим внимание, что контекст включает в себя не только переменные, но и место в коде, так что когда вложенный вызов завершится -- можно будет легко вернуться назад.

Слово «строка» здесь условно, на самом деле, конечно, запомнено более точное место в цепочке команд.

pow(2, 1)

Опять вложенный вызов в строке 3, на этот раз – с аргументами x=2, n=1. Создаётся новый текущий контекст, предыдущий добавляется в стек:

• Контекст: { x: 2, n: 3, строка 3 }
• Контекст: { x: 2, n: 2, строка 3 }
• Контекст: { x: 2, n: 1, строка 1 }

На текущий момент в стеке уже два старых контекста.

Выход из pow(2, 1).

При выполнении pow(2, 1), в отличие от предыдущих запусков, выражение n != 1 будет равно false, поэтому сработает вторая ветка if..else:

Здесь вложенных вызовов нет, так что функция заканчивает свою работу, возвращая 2. Текущий контекст больше не нужен и удаляется из памяти, из стека восстанавливается предыдущий:

• Контекст: { x: 2, n: 3, строка 3 }
• Контекст: { x: 2, n: 2, строка 3 }

Возобновляется обработка внешнего вызова `pow(2, 2)`.

Выход из pow(2, 2).

…И теперь уже pow(2, 2) может закончить свою работу, вернув 4. Восстанавливается контекст предыдущего вызова:

• Контекст: { x: 2, n: 3, строка 3 }

Возобновляется обработка внешнего вызова `pow(2, 3)`.

Выход из pow(2, 3).

Самый внешний вызов заканчивает свою работу, его результат: pow(2, 3) = 8.

Глубина рекурсии в данном случае составила: 3.

Как видно из иллюстраций выше, глубина рекурсии равна максимальному числу контекстов, одновременно хранимых в стеке.

Обратим внимание на требования к памяти. Рекурсия приводит к хранению всех данных для неоконченных внешних вызовов в стеке, в данном случае это приводит к тому, что возведение в степень n хранит в памяти n различных контекстов.

Реализация возведения в степень через цикл гораздо более экономна:

У такой функции pow будет один контекст, в котором будут последовательно меняться значения i и result.

Любая рекурсия может быть переделана в цикл. Как правило, вариант с циклом будет эффективнее.

Но переделка рекурсии в цикл может быть нетривиальной, особенно когда в функции, в зависимости от условий, используются различные рекурсивные подвызовы, когда ветвление более сложное.

Итого

Рекурсия – это когда функция вызывает сама себя, как правило, с другими аргументами.

Существуют много областей применения рекурсивных вызовов. Здесь мы посмотрели на один из них – решение задачи путём сведения её к более простой (с меньшими аргументами), но также рекурсия используется для работы с «естественно рекурсивными» структурами данных, такими как HTML-документы, для «глубокого» копирования сложных объектов.